1.0 LITAR SIRI
c. Hasil campur semua voltan susut di setiap perintang adalah bersamaan dengan voltan sumber.
d. Jumlah perintang di dalam litar siri adalah hasil campur kesemua nilai perintang di dalam litar.
b. Sekiranya diberi Vt dan Rt, arus keseluruhan litar It boleh dikira menggunakan rumus berikut:
It = Vt
Rt
c. Apabila, salah satu voltan susut diketahui maka arus boleh dikira menggunakan formula seperti di bawah :
I = Vr
R
d. Jika nilai arus total diberi, kita dapat menentukan nilai voltan susut melintangi setiap perintang dengan ….
Vr = ItR
e. Polariti voltan susut pada perintang adalah ditandakan sebagai positif apabila salah satu hujung perintang berhampiran dengan terminal positif punca bekalan.
f. Arus yang melalui perintang adalah pada arah positif perintang ke arah negative perintang.
g. Apabila terdapat, buka di dalam litar siri maka akan menghalang pengaliran arus oleh itu tiada susut voltan pada setiap perintang. Kita akan perolehi nilai voltan total pada point yang terbuka itu.
Contoh Penggunaan Hukum Ohm Di Dalam Litar Siri
1. Merujuk kepada litar di bawah, kirakan arus di dalam litar siri.
Dapatkan nilai Rt terlebih dahulu
RT = R1 + R2 + R3 + R4
= 82W + 22W + 15W + 10W
= 129W
Dengan menggunakan Hukum Ohm, kirakan nilai arus.
I =Vs
Rt
= 25
129
= 0.194A @ 194mA
2. Diberi nilai arus 1mA, kira Vs berdasarkan kepada litar di bawah.
Tentukan nilai Rt
Rt = 1.2kW + 5.6kW + 1.2kW + 1.5kW
= 9.5kW
Gunakan Hukum Ohm untuk dapatkan Vs
Vs = IRt
= (1mA)(9.5kW)
= 9.5V
1.6 HUKUM KIRCHHOFF VOLTAN (HKV)
HKV merupakan hukum litar asas yang menyatakan jumlah algebra bagi voltan di dalam satu litar yang tertutup adalah bersamaan dengan sifar ataupun jumlah voltan susut adalah sama dengan voltan bekalan.
Berikut bagaimana HKV didefinasikan :
a. Jumlah kesemua voltan susut di dalam satu litar tertutup adalah bersamaan dengan voltan sumber di dalam gelung tersebut.
Vs = V1 + V2 + V3 + . . . . . + Vn
b. Jumlah algebra bagi nilai voltan ( voltan susut dan voltan sumber ) di dalam satu laluan tertutup adalah bersamaan dengan sifar.
Vs – V1 –V2 – V3 – . . . . . – Vn = 0
Gambarajah di bawah menunjukkan secara jelas HKV.
1.7 PEMBAHAGI VOLTAN
Satu litar siri juga bertindak sebagi pembahagi voltan. Di mana arus yang melalui setiap perintang di dalam litar siri adalah sama oleh itu voltan susut adalah berkadaran dengan nilai rintangan.
Sekiranya didefinasikan secara jelas ialah jumlah keseluruhan voltan susut dibahagikan dengan jumlah rintangan adalah berkadaran terus dengan nilai rintangan tersebut.
Formula Umum Bagi Pembahagi Voltan Di Dalam Litar Siri.
2.0 LITAR SELARI
2.1 MENGENALPASTI LITAR SELARI
Didalam satu litar selari, laluan arus adalah dikenali sebagai cabang. Litar selari adalah litar yang mempunyai dua atau lebih cabang atau simpang. Arus yang mengalir dari punca bekalan akan membahagi pada setiap simpang dengan bertambahnya perintang atau beban yang disambung secara selari di dalam litar.
Litar selari adalah, litar yang mempunyai lebih daripada satu cabang di antara dua titik yang terpisah. Sekiranya, terdapat voltan antara dua titik pada cabang tersebut maka ia juga adalah litar selari diantara dua titik tersebut.
2.2 CIRI-CIRI LITAR SELARI
a. Voltan yang merentangi setiap perintang adalah sama dengan nilai voltan bekalan.
b. Arus yang melalui setiap perintang adalah tidak sama bergantung kepada nilai perintang.
c. Jumlah arus yang masuk ke tiap-tiap cabang adalah sama dengan jumlah arus keseluruhan dalam litar tersebut.
d. Jumlah rintangan di dalam litar selari adalah lebih rendah daripada nilai rintangan yang terkecil di dalam litar.
2.3 VOLTAN DI DALAM LITAR SELARI
Seperti yang diketahui, setiap laluan arus di dalam litar selari adalah dikenali sebagai simpang / cabang. Voltan yang merentangi setiap cabang adalah bersamaan dengan nilai voltan bekalan bagi litar tersebut.
Merujuk kepada rajah di atas, bateri sebagai sumber dibekalkan kepada litar merentangi tiga perintang yang disambung secara selari. Apabila voltan diukur merentangi voltan sumber dan setiap perintang, di dapati bacaan nilai voltan adalah sama.
CONTOH :
Tentukan nilai voltan yang merentangi setiap perintang.
V1 = V2 = V3 = V4 = V5 = Vs = 25V
Didapati terdapat lima perintang disambung secara selari, oleh itu voltan merentangi setiap perintang adalah sama dengan voltan bekalan bagi litar tersebut.
2.4 HUKUM KIRCHHOFF ARUS (HKA)
HKA boleh didefinasikan sebagai jumlah arus yang melalui suatu simpang adalah bersamaan dengan nilai arus yang keluar daripada simpang tersebut. Simpang di dalam litar selari adalah titik di mana dua atau lebih kompenen disambungkan.
Merujuk kepada gambarajah di atas, didapati arus daripada sumber It masuk ke simpang A dan arus terpisah kepada tiga cabang iaitu I1, I2 dan I3. Setiap arus tersebut adalah keluar daripada titik A, oleh itu ;
It = I1 +12 + I3
Arus-arus tersebut mengalir di dalam litar melalui cabang-cabang tersebut, kita dapat lihat arus tersebut balik kepada simpang B. Arus I1, I2 dan I3 masuk ke simpang B dan It keluar daripada simpang tersebut, oleh itu ;
I1 +12 + I3 = It
2.5 RUMUS UMUM BAGI HKA
Iin(1) + Iin(2) + Iin(3) + …. Iin(n) = Iout(1) + Iout(2) + Iout(3) + …. + Iout(m)
Iin(1) + Iin(2) + Iin(3) + Iin(n) - Iout(1) - Iout(2) - Iout(3) - Iout(m) = 0
HKA juga boleh didefinasikan sebagai jumlah algebra arus yang masuk dan keluar daripada simpang tersebut adalah bersamaan dengan nilai sifar,0.
Contoh :
Diberi nilai arus bagi setiap cabang litar, Tentukan nilai arus yang masuk ke simpang A dan juga nilai arus yang keluar daripada B.
Pada simpang A;
It = I1 + I2
= 5mA + 12mA
= 17mA
Pada simpang B;
I1 + I2 = It
5mA + 12mA = It
17mA = It
***It = 17mA
2.6 RINTANGAN DI DALAM LITAR SELARI
Apabila perintang disambungkan kepada litar selari maka jumlah nilai rintangan bagi litar tersebut adalah berkurangan. Jumlah rintangan keseluruhan adalah lebih kecil daripada nilai perintang terkecil di dalam litar tersebut.
Katakanlah juga bahawa Rl = 7 ohm, R2 = 10 ohm, R3 = 6 ohm dan R4 = 4 ohm.
* Pertama, litar itu dilukis semula dan cabang siri perintang R3 dan R4 digabungkan melalui campuran untuk membentuk satu rintangan persamaan Ra.
Ra = R3 + R4
= 6 + 4
= 10 ohm.
* Berikutnya, gabungan selari bagi R2 dan Ra digabungkan (menggunakan formula rintangan selari) sebagai rintangan persamaan Rb.
Rb = R2 x Ra
R2 + Ra
= 10 x 10
10 + 10
= 5 ohm.
* Akhir sekali, perintang sesiri Rl dicampurkan kepada rintangan persamaan Rb bagi gabungan selari untuk mendapatkan jumlah rintangan litar, RT.
Rt = Rl + Rb
= 7 + 5
= 12 ohm
* Dengan lain-lain perkataan, kesemua litar kompleks boleh dipecahkan dan diringkaskan sehingga RT = jumlah rintangan bagi litar sesiri-selari = 12 ohm.
3.2 MENGIRA ARUS
Sekiranya di beri nilai rintangan jumlah, RT dan nilai voltan bekalan, VS, maka nilai arus di dalam litar boleh dikira.Rumus bagi mencari nilai arus adalah seperti berikut :
3.2.1 ARUS SIMPANG
Dengan menggunakan rumus pembahagi arus, HKA, Hukum Ohm ataupun gabungan tersebut, nilai arus bagi cabang tertentu di dalam litar siri-selari boleh dicari.
Dapatkan arus yang memasuki simpang A. Untuk mendapatkan nilai arus litar, IT maka nilai RT perlu diperolehi terlebih dahulu.
Rt = R1 + R2R3 / R2 + R3
= 1.0kW + (2.2kW)(3.3kW) / (2.2kW) + (3.3kW)
= 1.0kW + 1.32kW
= 2.32kW
It = Vs / Rt
= 22V / 2.32kW
= 9.48mA
Dengan menggunakan pembahagi arus, nilai arus yang melalui perintang R2 dan R3 boleh dicari :
I2 = (R3 / R2 + R3 ) It
= ( 3.3kW / 5.5kW) 9.48mA
= 5.69mA
HKA digunakan untuk mendapatkan nilai bagi arus yang mengalir melalui I3
It = I2 + I3
I3 = It – I2
= 9.48mA – 5.69mA
= 3.79mA
3.2.2 KEJATUHAN VOLTAN
Pada litar siri-selari, kejatuhan voltan boleh dikira dengan mengaplikasikan beberapa formula yang telah dipelajari seperti formula Pembahagi Voltan, HKV, Hukum Ohm ataupun kombinasi daripada formul-formula tersebut.
Merujuk litar di atas, kirakan kejatuhan voltan pada setiap perintang tersebut.
Selarikan perintang R2 dan R3
R23 = R2 // R3
= 560W // 560W
= 280W
Rt = R1 + R23
= 150W + 280W
= 430W
Guna formula Pembahagi Voltan untuk mendapatkan kejatuhan voltan pada R23.
V23 = (R23 / Rt ) Vs
= ( 280W / 430W) x 80
= 52.1V = VR2 = VR3
ini adalah kerana perintang R2 dan R3 adalah selari maka voltannya adalah sama bagi setiap perintang.
Untuk mendapatkan kejatuhan voltan pada R1 dengan menggunakan HKV,
Vs = V1 + V23
V1 = Vs - V23
= 80 – 52.1
= 27.9V
1.1 Mengenalpasti Litar Siri
Litar siri ialah litar elektrik yang mempunyai cuma satu laluan arus di antara dua punca, jadi arus yang melalui setiap perintang adalah sama. Berikut merupakan perintang-perintangan yang disambung secara siri.
Litar siri ialah litar elektrik yang mempunyai cuma satu laluan arus di antara dua punca, jadi arus yang melalui setiap perintang adalah sama. Berikut merupakan perintang-perintangan yang disambung secara siri.
Manakala, gambarajah berikut menunjukkan laluan arus di dalam litar siri elektrik. Di mana kita dapati cuma ada satu laluan arus daripada titik A ke titik B.
1.2 Ciri-ciri Litar Siri
a. Nilai arus melalui setiap perintang adalah sama.
1.2 Ciri-ciri Litar Siri
a. Nilai arus melalui setiap perintang adalah sama.
b. Voltan susut melintangi setiap perintang adalah tidak sama bergantung kepada nilai perintang.
c. Hasil campur semua voltan susut di setiap perintang adalah bersamaan dengan voltan sumber.
d. Jumlah perintang di dalam litar siri adalah hasil campur kesemua nilai perintang di dalam litar.
1.3 ARUS DI DALAM LITAR SIRI
Arus adalah sama di setiap point pada litar siri. Arus yang melalui setiap perintang adalah sama dengan arus yang mengalir pada perintang-perintang lain.
1.4 RINTANGAN DI DALAM LITAR SIRI
Jumlah rintangan di dalam litar siri ialah hasil tambah bagi setiap nilai perintang di dalam litar siri. Semakin tinggi nilai rintangan di dalam litar, semakin banyak tentangan terhadap arus.
Rt = R1 + R2 + R3 + . . . . . + Rn
Contoh 1 :
Contoh 2 :
Tentukan nilai R4 ?
Rt = R1 + R2 + R3 + R4
R4 = Rt - ( R1 + R2 + R3 )
= 17.9kW– ( 1.0kW + 2.2kW + 4.7kW )
= 10kW
Arus adalah sama di setiap point pada litar siri. Arus yang melalui setiap perintang adalah sama dengan arus yang mengalir pada perintang-perintang lain.
1.4 RINTANGAN DI DALAM LITAR SIRI
Jumlah rintangan di dalam litar siri ialah hasil tambah bagi setiap nilai perintang di dalam litar siri. Semakin tinggi nilai rintangan di dalam litar, semakin banyak tentangan terhadap arus.
Rt = R1 + R2 + R3 + . . . . . + Rn
Contoh 1 :
Rt = R1 + R2 + R3 + R4 + R5
= 56W + 100W + 27W + 10W + 47W
= 240W
Contoh 2 :
Tentukan nilai R4 ?
Rt = R1 + R2 + R3 + R4
R4 = Rt - ( R1 + R2 + R3 )
= 17.9kW– ( 1.0kW + 2.2kW + 4.7kW )
= 10kW
1.5 HUKUM OHM DALAM LITAR SIRI
Berikut merupakan beberapa kata kunci untuk diingatkan apabila menganalisa litar siri.
a. Arus yang melalui sesuatu perintang adalah sama pada setiap perintang yang
lain, ia adalah arus keseluruhan litar.
Berikut merupakan beberapa kata kunci untuk diingatkan apabila menganalisa litar siri.
a. Arus yang melalui sesuatu perintang adalah sama pada setiap perintang yang
lain, ia adalah arus keseluruhan litar.
b. Sekiranya diberi Vt dan Rt, arus keseluruhan litar It boleh dikira menggunakan rumus berikut:
It = Vt
Rt
c. Apabila, salah satu voltan susut diketahui maka arus boleh dikira menggunakan formula seperti di bawah :
I = Vr
R
d. Jika nilai arus total diberi, kita dapat menentukan nilai voltan susut melintangi setiap perintang dengan ….
Vr = ItR
e. Polariti voltan susut pada perintang adalah ditandakan sebagai positif apabila salah satu hujung perintang berhampiran dengan terminal positif punca bekalan.
f. Arus yang melalui perintang adalah pada arah positif perintang ke arah negative perintang.
g. Apabila terdapat, buka di dalam litar siri maka akan menghalang pengaliran arus oleh itu tiada susut voltan pada setiap perintang. Kita akan perolehi nilai voltan total pada point yang terbuka itu.
Contoh Penggunaan Hukum Ohm Di Dalam Litar Siri
1. Merujuk kepada litar di bawah, kirakan arus di dalam litar siri.
Dapatkan nilai Rt terlebih dahulu
RT = R1 + R2 + R3 + R4
= 82W + 22W + 15W + 10W
= 129W
Dengan menggunakan Hukum Ohm, kirakan nilai arus.
I =Vs
Rt
= 25
129
= 0.194A @ 194mA
2. Diberi nilai arus 1mA, kira Vs berdasarkan kepada litar di bawah.
Tentukan nilai Rt
Rt = 1.2kW + 5.6kW + 1.2kW + 1.5kW
= 9.5kW
Gunakan Hukum Ohm untuk dapatkan Vs
Vs = IRt
= (1mA)(9.5kW)
= 9.5V
1.6 HUKUM KIRCHHOFF VOLTAN (HKV)
HKV merupakan hukum litar asas yang menyatakan jumlah algebra bagi voltan di dalam satu litar yang tertutup adalah bersamaan dengan sifar ataupun jumlah voltan susut adalah sama dengan voltan bekalan.
Berikut bagaimana HKV didefinasikan :
a. Jumlah kesemua voltan susut di dalam satu litar tertutup adalah bersamaan dengan voltan sumber di dalam gelung tersebut.
Vs = V1 + V2 + V3 + . . . . . + Vn
b. Jumlah algebra bagi nilai voltan ( voltan susut dan voltan sumber ) di dalam satu laluan tertutup adalah bersamaan dengan sifar.
Vs – V1 –V2 – V3 – . . . . . – Vn = 0
Gambarajah di bawah menunjukkan secara jelas HKV.
1.7 PEMBAHAGI VOLTAN
Satu litar siri juga bertindak sebagi pembahagi voltan. Di mana arus yang melalui setiap perintang di dalam litar siri adalah sama oleh itu voltan susut adalah berkadaran dengan nilai rintangan.
Sekiranya didefinasikan secara jelas ialah jumlah keseluruhan voltan susut dibahagikan dengan jumlah rintangan adalah berkadaran terus dengan nilai rintangan tersebut.
Formula Umum Bagi Pembahagi Voltan Di Dalam Litar Siri.
2.0 LITAR SELARI
2.1 MENGENALPASTI LITAR SELARI
Didalam satu litar selari, laluan arus adalah dikenali sebagai cabang. Litar selari adalah litar yang mempunyai dua atau lebih cabang atau simpang. Arus yang mengalir dari punca bekalan akan membahagi pada setiap simpang dengan bertambahnya perintang atau beban yang disambung secara selari di dalam litar.
Litar selari adalah, litar yang mempunyai lebih daripada satu cabang di antara dua titik yang terpisah. Sekiranya, terdapat voltan antara dua titik pada cabang tersebut maka ia juga adalah litar selari diantara dua titik tersebut.
2.2 CIRI-CIRI LITAR SELARI
a. Voltan yang merentangi setiap perintang adalah sama dengan nilai voltan bekalan.
b. Arus yang melalui setiap perintang adalah tidak sama bergantung kepada nilai perintang.
c. Jumlah arus yang masuk ke tiap-tiap cabang adalah sama dengan jumlah arus keseluruhan dalam litar tersebut.
d. Jumlah rintangan di dalam litar selari adalah lebih rendah daripada nilai rintangan yang terkecil di dalam litar.
2.3 VOLTAN DI DALAM LITAR SELARI
Seperti yang diketahui, setiap laluan arus di dalam litar selari adalah dikenali sebagai simpang / cabang. Voltan yang merentangi setiap cabang adalah bersamaan dengan nilai voltan bekalan bagi litar tersebut.
Merujuk kepada rajah di atas, bateri sebagai sumber dibekalkan kepada litar merentangi tiga perintang yang disambung secara selari. Apabila voltan diukur merentangi voltan sumber dan setiap perintang, di dapati bacaan nilai voltan adalah sama.
CONTOH :
Tentukan nilai voltan yang merentangi setiap perintang.
V1 = V2 = V3 = V4 = V5 = Vs = 25V
Didapati terdapat lima perintang disambung secara selari, oleh itu voltan merentangi setiap perintang adalah sama dengan voltan bekalan bagi litar tersebut.
2.4 HUKUM KIRCHHOFF ARUS (HKA)
HKA boleh didefinasikan sebagai jumlah arus yang melalui suatu simpang adalah bersamaan dengan nilai arus yang keluar daripada simpang tersebut. Simpang di dalam litar selari adalah titik di mana dua atau lebih kompenen disambungkan.
Merujuk kepada gambarajah di atas, didapati arus daripada sumber It masuk ke simpang A dan arus terpisah kepada tiga cabang iaitu I1, I2 dan I3. Setiap arus tersebut adalah keluar daripada titik A, oleh itu ;
It = I1 +12 + I3
Arus-arus tersebut mengalir di dalam litar melalui cabang-cabang tersebut, kita dapat lihat arus tersebut balik kepada simpang B. Arus I1, I2 dan I3 masuk ke simpang B dan It keluar daripada simpang tersebut, oleh itu ;
I1 +12 + I3 = It
2.5 RUMUS UMUM BAGI HKA
Iin(1) + Iin(2) + Iin(3) + …. Iin(n) = Iout(1) + Iout(2) + Iout(3) + …. + Iout(m)
Atau
Iin(1) + Iin(2) + Iin(3) + Iin(n) - Iout(1) - Iout(2) - Iout(3) - Iout(m) = 0
HKA juga boleh didefinasikan sebagai jumlah algebra arus yang masuk dan keluar daripada simpang tersebut adalah bersamaan dengan nilai sifar,0.
Contoh :
Diberi nilai arus bagi setiap cabang litar, Tentukan nilai arus yang masuk ke simpang A dan juga nilai arus yang keluar daripada B.
Pada simpang A;
It = I1 + I2
= 5mA + 12mA
= 17mA
Pada simpang B;
I1 + I2 = It
5mA + 12mA = It
17mA = It
***It = 17mA
2.6 RINTANGAN DI DALAM LITAR SELARI
Apabila perintang disambungkan kepada litar selari maka jumlah nilai rintangan bagi litar tersebut adalah berkurangan. Jumlah rintangan keseluruhan adalah lebih kecil daripada nilai perintang terkecil di dalam litar tersebut.
Persamaan bagi nilai rintangan dalam litar selari ;
Persamaan mudah untuk jumlah nilai rintangan bagi kes ;
1. Dua perintang di dalam litar
2. Perintang-perintang yang mempunyai sama nilai di dalam litar
Di mana,
n adalah bilangan perintang di dalam litar.
3. Menentukan nilai perintang yang tidak diketahui
Di mana,
Rx adalah nilai rintangan yang tidak diketahui.
2.7 PEMBAHAGI ARUS
Litar selari bertindak sebagai pembahagi arus kerana arus yang memasuki simpang pada cabang selari membahagi kepada setiap sejumlah cabang arus tertentu. Berikut menunjukan prinsip pembahagian arus di dalam litar selari ;
Voltan yang merentangi setiap perintang di dalam litar selari adalah sama manakala arus cabang adalah berkadar songsang dengan nilai perintang pada cabang tersebut. Pada cabang yang mempunyai rintangan tinggi, arusnya adalah kurang berbanding cabang yang mempunyai rintangan rendah.
2.8 RUMUS PEMBAHAGI ARUS
a. Litar Selari Dua Cabang
b. Mana-mana Cabang Arus
Arus ( Ix ) yang mengalir melalui mana-mana cabang adalah bersamaan dengan jumlah rintangan keseluruhan ( Rt ) dibahagikan dengan rintangan cabang tersebut ( Rx ) dan didarabkan dengan arus keseluruhan ( It ) yang memasuki simpang cabang litar selari.
3.0 LITAR SIRI-SELARI
Litar gabungan ini mungkin siri dalam selari atau selari dalam siri. Bagi litar siri dalam selari, litar siri perlu diselesaikan dahulu sebelum litar selari, begitu juga sebaliknya.
* Litar siri dalam selari * Litar selari dalam siri
Tidak ada formula baru diperlukan untuk mencari jumlah rintangan bagi perintang yang disambungkan dalam siri-selari. Apa yang perlu ialah memecahkan litar yang lengkap kepada bahagian-bahagian, tiap-tiap satu mengandungi litar siri dan litar selari yang mudah. Kemudian selesaikan tiap-tiap satu secara berasingan dan gabungkan jawapannya. Tetapi sebelum menggunakan peraturan-peraturan bagi rintangan siri dan selari, mestilah terlebih dahulu ditentukan cara yang baik untuk meringkaskan litar itu.
LANGKAH-LANGKAH MERINGKAS LITAR
Oleh itu, langkah-langkah asas mencari jumlah rintangan bagi satu litar siri-selari yang kompleks adalah seperti berikut:
1. Melukis semula litar itu jika perlu.
2. Jika mana-mana gabungan selari mempunyai cabang yang mengandungi dua atau lebih perintang sesiri, cari jumlah nilai bagi perintang ini dengan mencampurkannya.
3. Dengan menggunakan formula rintangan selari cari jumlah rintangan bahagian-bahagian selari litar.
4. Campurkan rintangan gabungan selari kepada mana-mana rintangan yang sesiri dengannya.
3.1 MENGIRA JUMLAH RINTANGAN DALAM LITAR, Rt
Berikut adalah contoh bagaimana memecahkan litar-litar kompleks untuk mendapatkan jumlah rintangan.
* Katakan litar anda mengandungi empat perintang: Rl, R2, R3 dan R4 disambungkan seperti yang ditunjukkan. Anda ingin mencari jumlah rintangan litar.
atau
Persamaan mudah untuk jumlah nilai rintangan bagi kes ;
1. Dua perintang di dalam litar
2. Perintang-perintang yang mempunyai sama nilai di dalam litar
Rt = R / n
Di mana,
n adalah bilangan perintang di dalam litar.
3. Menentukan nilai perintang yang tidak diketahui
Rx = RaRt / Ra – Rt
Di mana,
Rx adalah nilai rintangan yang tidak diketahui.
2.7 PEMBAHAGI ARUS
Litar selari bertindak sebagai pembahagi arus kerana arus yang memasuki simpang pada cabang selari membahagi kepada setiap sejumlah cabang arus tertentu. Berikut menunjukan prinsip pembahagian arus di dalam litar selari ;
Voltan yang merentangi setiap perintang di dalam litar selari adalah sama manakala arus cabang adalah berkadar songsang dengan nilai perintang pada cabang tersebut. Pada cabang yang mempunyai rintangan tinggi, arusnya adalah kurang berbanding cabang yang mempunyai rintangan rendah.
2.8 RUMUS PEMBAHAGI ARUS
a. Litar Selari Dua Cabang
b. Mana-mana Cabang Arus
Arus ( Ix ) yang mengalir melalui mana-mana cabang adalah bersamaan dengan jumlah rintangan keseluruhan ( Rt ) dibahagikan dengan rintangan cabang tersebut ( Rx ) dan didarabkan dengan arus keseluruhan ( It ) yang memasuki simpang cabang litar selari.
3.0 LITAR SIRI-SELARI
Litar gabungan ini mungkin siri dalam selari atau selari dalam siri. Bagi litar siri dalam selari, litar siri perlu diselesaikan dahulu sebelum litar selari, begitu juga sebaliknya.
* Litar siri dalam selari * Litar selari dalam siri
Tidak ada formula baru diperlukan untuk mencari jumlah rintangan bagi perintang yang disambungkan dalam siri-selari. Apa yang perlu ialah memecahkan litar yang lengkap kepada bahagian-bahagian, tiap-tiap satu mengandungi litar siri dan litar selari yang mudah. Kemudian selesaikan tiap-tiap satu secara berasingan dan gabungkan jawapannya. Tetapi sebelum menggunakan peraturan-peraturan bagi rintangan siri dan selari, mestilah terlebih dahulu ditentukan cara yang baik untuk meringkaskan litar itu.
LANGKAH-LANGKAH MERINGKAS LITAR
Oleh itu, langkah-langkah asas mencari jumlah rintangan bagi satu litar siri-selari yang kompleks adalah seperti berikut:
1. Melukis semula litar itu jika perlu.
2. Jika mana-mana gabungan selari mempunyai cabang yang mengandungi dua atau lebih perintang sesiri, cari jumlah nilai bagi perintang ini dengan mencampurkannya.
3. Dengan menggunakan formula rintangan selari cari jumlah rintangan bahagian-bahagian selari litar.
4. Campurkan rintangan gabungan selari kepada mana-mana rintangan yang sesiri dengannya.
3.1 MENGIRA JUMLAH RINTANGAN DALAM LITAR, Rt
Berikut adalah contoh bagaimana memecahkan litar-litar kompleks untuk mendapatkan jumlah rintangan.
* Katakan litar anda mengandungi empat perintang: Rl, R2, R3 dan R4 disambungkan seperti yang ditunjukkan. Anda ingin mencari jumlah rintangan litar.
Katakanlah juga bahawa Rl = 7 ohm, R2 = 10 ohm, R3 = 6 ohm dan R4 = 4 ohm.
* Pertama, litar itu dilukis semula dan cabang siri perintang R3 dan R4 digabungkan melalui campuran untuk membentuk satu rintangan persamaan Ra.
Ra = R3 + R4
= 6 + 4
= 10 ohm.
* Berikutnya, gabungan selari bagi R2 dan Ra digabungkan (menggunakan formula rintangan selari) sebagai rintangan persamaan Rb.
Rb = R2 x Ra
R2 + Ra
= 10 x 10
10 + 10
= 5 ohm.
* Akhir sekali, perintang sesiri Rl dicampurkan kepada rintangan persamaan Rb bagi gabungan selari untuk mendapatkan jumlah rintangan litar, RT.
Rt = Rl + Rb
= 7 + 5
= 12 ohm
* Dengan lain-lain perkataan, kesemua litar kompleks boleh dipecahkan dan diringkaskan sehingga RT = jumlah rintangan bagi litar sesiri-selari = 12 ohm.
3.2 MENGIRA ARUS
Sekiranya di beri nilai rintangan jumlah, RT dan nilai voltan bekalan, VS, maka nilai arus di dalam litar boleh dikira.Rumus bagi mencari nilai arus adalah seperti berikut :
VS
IT = ---------
RT
3.2.1 ARUS SIMPANG
Dengan menggunakan rumus pembahagi arus, HKA, Hukum Ohm ataupun gabungan tersebut, nilai arus bagi cabang tertentu di dalam litar siri-selari boleh dicari.
Dapatkan arus yang memasuki simpang A. Untuk mendapatkan nilai arus litar, IT maka nilai RT perlu diperolehi terlebih dahulu.
Rt = R1 + R2R3 / R2 + R3
= 1.0kW + (2.2kW)(3.3kW) / (2.2kW) + (3.3kW)
= 1.0kW + 1.32kW
= 2.32kW
It = Vs / Rt
= 22V / 2.32kW
= 9.48mA
Dengan menggunakan pembahagi arus, nilai arus yang melalui perintang R2 dan R3 boleh dicari :
I2 = (R3 / R2 + R3 ) It
= ( 3.3kW / 5.5kW) 9.48mA
= 5.69mA
HKA digunakan untuk mendapatkan nilai bagi arus yang mengalir melalui I3
It = I2 + I3
I3 = It – I2
= 9.48mA – 5.69mA
= 3.79mA
3.2.2 KEJATUHAN VOLTAN
Pada litar siri-selari, kejatuhan voltan boleh dikira dengan mengaplikasikan beberapa formula yang telah dipelajari seperti formula Pembahagi Voltan, HKV, Hukum Ohm ataupun kombinasi daripada formul-formula tersebut.
Merujuk litar di atas, kirakan kejatuhan voltan pada setiap perintang tersebut.
Selarikan perintang R2 dan R3
R23 = R2 // R3
= 560W // 560W
= 280W
Rt = R1 + R23
= 150W + 280W
= 430W
Guna formula Pembahagi Voltan untuk mendapatkan kejatuhan voltan pada R23.
V23 = (R23 / Rt ) Vs
= ( 280W / 430W) x 80
= 52.1V = VR2 = VR3
ini adalah kerana perintang R2 dan R3 adalah selari maka voltannya adalah sama bagi setiap perintang.
Untuk mendapatkan kejatuhan voltan pada R1 dengan menggunakan HKV,
Vs = V1 + V23
V1 = Vs - V23
= 80 – 52.1
= 27.9V























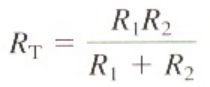

















Tiada ulasan:
Catat Ulasan